How big is that molecule in the window

Down in the comments Peter Ridley makes believe that Eli is Bob Grumbine and asks

I need some help with regard to the size of gas molecules and adsorption of atmospheric gases. I understand that you are a specialist in this area so can you give me a link or two to relevant sites/papers?

Eli is touched by Peter, for asking these two subtle and complicated questions. The Bunny will try at least to get started. Climbing into the wayback machine and setting the dial to Gen Chem 1, we find (and you can find this in an Gen Chem or Physics book and even the Wikipedia) that a wide range of the behavior of gases can be described by what is called the ideal gas law, the three assumptions of which reverse Peter's questions. In an ideal gas

1. The size of the molecules is zero
2. They do not interact
3. They move randomly, with a Maxwellian velocity distribution

Clicking on the link takes you to a nice applet demonstrating ideal gas behavior at Oklahoma State, a small, but significant apology Eli supposes for Darryl Imhofe.

Simply looking at the three assumptions of the ideal gas law tells us that molecular size is a measure of the interaction between molecules since size measures in some way the distance that they begin to significantly interact at. So what are the forces involved? Although spin plays a role, intermolecular forces are electrical forces, the repulsion of the negatively charged electrons for each other and their attraction to the positive nuclei, as well as the mutual repulsion of the nuclei. As molecules approach each other the electrons rearrange themselves under the influence of the positive and negative charges in the other molecule. The details differ, depending on whether ions, molecules with net charge, are involved, or polar molecules, molecules where the charges sum to zero, but the are arranged a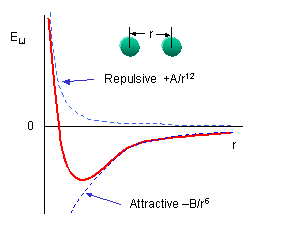symmetrically so there is a positive and a negatively charged end. The figure to the left shows the result of such rearrangement as two non polar molecules approach each other. The potential is called a 6-12 or Lennard-Jones potential describing the negative power of the attractive and repulsive potentials involved or the names of the folk who thought it up. It turns out to be a pretty good model for collisions of non-polar molecules when the density is low and demonstrates Peter's problem (Peter has a principle, why not a problem). On the one hand the ideal gas law works really well to describe the behavior of most atmospheric gases and its assumption is that the size of molecules is zero. On the other hand, our ball and stick picture of a molecule is as a hard sphere, or if the bunnies have been reading their textbook, a collection of hard spheres, but look at the potential, it extends to infinity!! because electrical attraction is unbounded. We get some hint of what to do by looking at the Lennard-Jones potential energy function for a collision of polar molecules

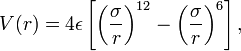The ε is a measure of the depth of the attractive part of the potential, the σ is the cross-sectional area of the collision, e.g. the size we are looking for. You can do similar things for collisions of polar molecules with each other or non-polar ones, or for ionic collisions, etc, at the cost of a more complex potential. These are all simple model potentials which fit a number of cases over impressive ranges of pressure and temperature, but they are models. The most accurate ways of finding the best fit require complex ab initio (first principles) quantum chemical calculations for specific collision partners, or simpler molecular mechanics models, but there you have to ask yourself, what do you mean by a collision, is a collision one in which velocity and quantum state don't change, but the direction of each molecule is changed, one in which the velocity changes, etc. Each of these will have different cross-sections, and thus, from Peter's POV a different "size"

Still, you can do very well with the 6-12 potential, or even a hard sphere potential, the question is how can the class find the cross-sections. The answer is surprisingly simple, measure the viscosity, measure the second Virial coefficient, measure any departure from the ideal gas law, because that is a measure of the range and the forces between molecular pairs in a collision.

This was the way molecular sizes were determined before large computers and molecular beam systems. Eli has a very old book, Molecular Theory of Gases and Liquids by Hischfelder Curtiss and Bird from 1952, which goes through such models in detail and has extensive tables of cross-sections derived from measurements. HOWEVER, probably the simplest way is to get thee to a computer with a molecular mechanics program such a pcmodel, or programs such as SPARTAN or Gaussian, and calculate the size of the molecule using potted subroutines.

Think of this as the start of a discussion.