How big is that molecule in the window
Down in the comments Peter Ridley makes believe that Eli is Bob Grumbine and asks
I need some help with regard to the size of gas molecules and adsorption of atmospheric gases. I understand that you are a specialist in this area so can you give me a link or two to relevant sites/papers?Eli is touched by Peter, for asking these two subtle and complicated questions. The Bunny will try at least to get started. Climbing into the wayback machine and setting the dial to Gen Chem 1, we find (and you can find this in an Gen Chem or Physics book and even the Wikipedia) that a wide range of the behavior of gases can be described by what is called the ideal gas law, the three assumptions of which reverse Peter's questions. In an ideal gas

- The size of the molecules is zero
- They do not interact
- They move randomly, with a Maxwellian velocity distribution
Simply looking at the three assumptions of the ideal gas law tells us that molecular size is a measure of the interaction between molecules since size measures in some way the distance that they begin to significantly interact at. So what are the forces involved? Although spin plays a role, intermolecular forces are electrical forces, the repulsion of the negatively charged electrons for each other and their attraction to the positive nuclei, as well as the mutual repulsion of the nuclei. As molecules approach each other the electrons rearrange themselves under the influence of the positive and negative charges in the other molecule. The details differ, depending on whether ions, molecules with net charge, are involved, or polar molecules, molecules where the charges sum to zero, but the are arranged a
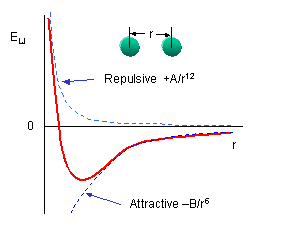 symmetrically so there is a positive and a negatively charged end. The figure to the left shows the result of such rearrangement as two non polar molecules approach each other. The potential is called a 6-12 or Lennard-Jones potential describing the negative power of the attractive and repulsive potentials involved or the names of the folk who thought it up. It turns out to be a pretty good model for collisions of non-polar molecules when the density is low and demonstrates Peter's problem (Peter has a principle, why not a problem). On the one hand the ideal gas law works really well to describe the behavior of most atmospheric gases and its assumption is that the size of molecules is zero. On the other hand, our ball and stick picture of a molecule is as a hard sphere, or if the bunnies have been reading their textbook, a collection of hard spheres, but look at the potential, it extends to infinity!! because electrical attraction is unbounded. We get some hint of what to do by looking at the Lennard-Jones potential energy function for a collision of polar molecules
symmetrically so there is a positive and a negatively charged end. The figure to the left shows the result of such rearrangement as two non polar molecules approach each other. The potential is called a 6-12 or Lennard-Jones potential describing the negative power of the attractive and repulsive potentials involved or the names of the folk who thought it up. It turns out to be a pretty good model for collisions of non-polar molecules when the density is low and demonstrates Peter's problem (Peter has a principle, why not a problem). On the one hand the ideal gas law works really well to describe the behavior of most atmospheric gases and its assumption is that the size of molecules is zero. On the other hand, our ball and stick picture of a molecule is as a hard sphere, or if the bunnies have been reading their textbook, a collection of hard spheres, but look at the potential, it extends to infinity!! because electrical attraction is unbounded. We get some hint of what to do by looking at the Lennard-Jones potential energy function for a collision of polar molecules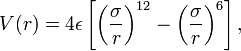 The ε is a measure of the depth of the attractive part of the potential, the σ is the cross-sectional area of the collision, e.g. the size we are looking for. You can do similar things for collisions of polar molecules with each other or non-polar ones, or for ionic collisions, etc, at the cost of a more complex potential. These are all simple model potentials which fit a number of cases over impressive ranges of pressure and temperature, but they are models. The most accurate ways of finding the best fit require complex ab initio (first principles) quantum chemical calculations for specific collision partners, or simpler molecular mechanics models, but there you have to ask yourself, what do you mean by a collision, is a collision one in which velocity and quantum state don't change, but the direction of each molecule is changed, one in which the velocity changes, etc. Each of these will have different cross-sections, and thus, from Peter's POV a different "size"
The ε is a measure of the depth of the attractive part of the potential, the σ is the cross-sectional area of the collision, e.g. the size we are looking for. You can do similar things for collisions of polar molecules with each other or non-polar ones, or for ionic collisions, etc, at the cost of a more complex potential. These are all simple model potentials which fit a number of cases over impressive ranges of pressure and temperature, but they are models. The most accurate ways of finding the best fit require complex ab initio (first principles) quantum chemical calculations for specific collision partners, or simpler molecular mechanics models, but there you have to ask yourself, what do you mean by a collision, is a collision one in which velocity and quantum state don't change, but the direction of each molecule is changed, one in which the velocity changes, etc. Each of these will have different cross-sections, and thus, from Peter's POV a different "size"Still, you can do very well with the 6-12 potential, or even a hard sphere potential, the question is how can the class find the cross-sections. The answer is surprisingly simple, measure the viscosity, measure the second Virial coefficient, measure any departure from the ideal gas law, because that is a measure of the range and the forces between molecular pairs in a collision.
This was the way molecular sizes were determined before large computers and molecular beam systems. Eli has a very old book, Molecular Theory of Gases and Liquids by Hischfelder Curtiss and Bird from 1952, which goes through such models in detail and has extensive tables of cross-sections derived from measurements. HOWEVER, probably the simplest way is to get thee to a computer with a molecular mechanics program such a pcmodel, or programs such as SPARTAN or Gaussian, and calculate the size of the molecule using potted subroutines.
Think of this as the start of a discussion.





17 comments:
Some of these hits look likely to be relevant history for this question, and may clarify the intent behind it.
http://www.google.com/search?q="Peter+Ridley"+gas+molecule+size+adsorption
Eli, I think you're being asked to help improve Taguchi's draft, as excerpted in this post. Hold out for a coauthorship, don't let yourself become a footnote.
http://chriscolose.wordpress.com/2009/10/26/consequences-of-being-over-concerned/#comment-1325
More like a football.
Eli, you should have suggested that Mr. Ridley get some crossed molecular beam machines and measure cross sections himself.
Well, it's actually an interesting question as the post shows and the answer teaches a great deal of physical chemistry, ranging from the gas laws to ab initio calculations to scattering experiments.
Besides which, Eli wants that crossed molecular beam system for Rabett Labs. Gotta put up a tip jar.
Hi Eli, I was just flying by and I thought I might leave you folks some easy reading and a short AV show for the class... put on the thinking caps, here we go!...
Have you ever wondered what holds everything together? Please read: I John 1:5-7, the Light does it all, for everything. Check out the Blue Letter Bible.com and do a study on the word, light. Very big study, good though. Now the AV short; if you have time?
http://www.youtube.com/watch?v=n426PazcFXE&feature=related
Lots to think about in a hurry, gotta fly...
Anonymous (the previous) isn't all wrong: photons do mediate the electromagnetic force which is key for holding molecules together (and therefore the size of particles as addressed in this post)... sadly, for anonymous you kind of also need the weak (bosons) and strong (gluon) forces to hold nuclei and atoms together, respectively. Gravity is kind of nice on the large scale too... I'm not sure about the current status of "gravitons" as a mediating particle, or whether general relativity makes particles superfluous for this force. But anyway, light isn't enough by itself is what I'm trying to say.
-Marcus
God never mentioned electrons
I knew you folks could see what we see..."But anyway, light isn't enough by itself is what I'm trying to say." Right On. Thanks Marcus
By-By
Dudley Herschbach is emeritus, so Eli might be able to get one of his used crossed beam machines cheap.
An interesting thing I've noticed about binary collisions is that the effective radius for such collisions tends to be related to the sum of the radii in most cases, as is intuitive. However, for collisions between atomic hydrogen and a larger atom/molecule, the effective collision radius is close to the H/H binary radius, as if the H just plowed along through the big guy as if it were some kind of nouvelle cuisine culinary foam. Any remarks to offer on that?
--raypierre
Fish: to Raypierre
Bare protons apparently aren't deflected by the electron shells of other atoms. They are apparently interacting with the other atom's nucleus. This makes sense because atoms with electron shells interact by the mutual repulsion of the negative charges of the electrons. A bare proton is not repelled by the electrons of the other atom.
Eli, thanks for starting this thread with some very helpful information which I will look at carefully. An anonymous blogger suggested on the original thread (Note 1) that I try using Google to get the answer. That was my first port of call after reading Jaworowski’s papers but it did not provide as much as I needed to resolve the issue of the validity of using air trapped in ice cores to reconstruct ancient atmospheric gas concentrations. That should answer your request for more details on QUOTE; .. what you want to know about adsorption, in particular what systems you are thinking about? UNQUOTE.
As Marco said I have been debating this issue on Chris Colose’s thread “Richard Alley at he AGU .. “ (Note 2) but only one person there tried to help (Marco could only comment in the same vein as on your other thread).
NOTES:
1) see http://rabett.blogspot.com/2010/03/too-bad-to-be-believed.html
2) see http://chriscolose.wordpress.com/2009/12/18/richard-alley-at-agu-2009-the-biggest-control-knob/
Regards, Pete R
RayP, hydrogen atoms are not very polarizable, and hydrogen is very light and it can tunnel through a small barrier. The polarizability of atoms scales inversely with the charge density, thus hydrogen could get pretty close to a neutral molecule before the dispersion forces took over.
Another thing which bears looking into is whether there is any charge exchange (this does happen with alkalai metals for example) in the entry channel, followed by neutralization on the way out. Have to think about this
Fish: Protons are charged. H atoms not.
RayP, that's a really interesting fact, which I was not aware of. In your examples, what sorts of atoms/molecules is the H atom colliding with ? That might help us to figure this out.
Eli, is polarizability really all that relevant here ? Sure, it contributes to R_e, but the effective collision diameter has comes primarily from the repulsive term (A/r^12 in the figure) which is determined by Pauli repulsion, not dispersion. Polarizability shows up in the attractive term (the coefficient of r^-6.) To be sure, decreasing the polarizability will tend to pull sigma, the point where the red curve crosses the x axis, outward, so there is some effect, but I don't think it's enough to explain RayP's observation.
But you're probably right about tunnelling. And charge transfer contributions seem very plausibl.
I think the key point is that H atom is *open shell*, which means we need to take chemical bonding types of interactions, which are not well described by Lennard-Jones, into account.
if we can find molecules that are smaller than the skin pores, then can that treat excessive sweating.. my science teacher said that we can use zinc to be waterproofed
Eli (and others who have tried to make constructive comments), thanks for your contributions so far. Every little helps (excluding childish schoolyard insults of course).
Hank (Roberts) your first comment is of no value at all and your second is way off the mark. My question has absolutely nothing to do with Roger Taguchi's paper.
While I research what has been offered so far could anyone consider the implications of all of this upon gases within the atmospheric as they are gradually “trapped” within a growing glacier?
Best regards, Pete R
Regards, Pete R
Post a Comment