High Pressure Limit. . . .
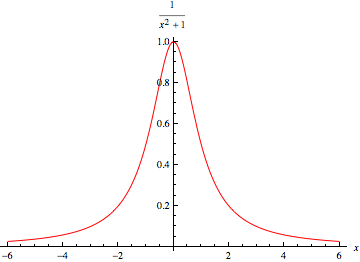
This is a continuation of playing with Eli's new chewy carrot colored Spectral Calculator toy the mice left in the burrow. A couple of days ago, the Rabetts looked at the effect of pressure, and before that temperature on CO2 bending mode absorption spectrum. Eli remarked on the fact that the peak of the pressure broadened absorption stays at about the same level for a constant volume mixing ratio above 50 mbar total pressure. This means that the peak of the absorption stays the same while the line gets wider, for example at 100 mbar and 1000 mbar total pressure and 380 ppm volume mixing ratio
The mice had a nice chatter about this. Eli wants to use this as a jumping off point.
There are three relevant line widths. The natural line width, which is a measure of the vibrationally excited state radiative lifetime and the associated uncertainty spread in the energy level. For vibrational lines these are sub MHz.
Since spectroscopy goes back and forth between MHz (very high resolution, microwave spectroscopy) and cm-1 (IR, visible, UV spectroscopy) we need an equivalence. Simply divide 1 MHz by the speed of light in cm/sec, 3 x 10^10 finding that 1 MHz is equivalent to 3.3 x 10^-5 cm-1.
The shape of the natural (isolated/no collisions) line is Lorentzian (from Wolfrum Mathworld).
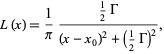
where the Gamma (the thing like the hangman uses) is the full line width at half maximum (FWHM).
The second linewidth that we have to worry about is the Doppler width. Doppler broadening is a shift in frequency when something (the molecule) is moving towards you (increase) or away from you (decrease). For emission or absorption of light the shift will be wo(1+v/c) where wo is the frequency of absorption/emission in the rest frame, v the speed along the direction the photon moves in and c the speed of light. When you average over all possible directions of molecular motion, this turns out to be Gaussian
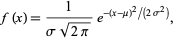
We can estimate the Doppler linewidth. The translational energy of the molecule is Et= 3/2 kT, where k is Boltzmann's constant, 1.38 x 10^-23 kg-m^2 /K-s^2. This yields Et= 6.2 x 10^-21 J, but we also know that Et= 1/2 m v^2, so v = sqrt(2Et/m) where m is in kg. The mass of one CO2 (C= 12 g/mole, O=16 g/mole. If you want to do this to four significant figures you don't have the one tru back of the envelope koan) molecule is 0.044 kg / 6.02 x 10^23 molecules/mole and we get that the velocity is ~ 400 m/s.
The speed of light is 3 x 10 ^8 m/s so v/c is 1 x 10^-6. For a 600 cm-1 transition (CO2 bend) this is about 1 x 10^-3 cm-1 or 30 MHz. The Doppler width varies directly with the frequency of the transition, so a transition at 6000 cm-1 would have a Doppler width that is ~300 MHz at room temperature.
Finally the line shape associated with collisional line broadening is also Lorentzian. The natural and collision broadened line shapes can be simply combined by setting the line width equal to the sum of the radiative and collisional terms. The collisional term is proportional to the total pressure in the binary collision limit (atmospheric, unless you deep down in Jupiter). The higher the pressure, the more collisions. Remember this.
Combining the Gaussian Doppler broadening with the Lorentzian radiative and collisional terms is trickier. The solution was first found by Armstrong, and is called the Voigt line profile. However, it should be clear that if the collisional broadening is >> than the Doppler broadening (0.001 cm-1 @ 300 K for the CO2 bend) and the Doppler broadening is >> the natural line width, we can neglect the foofaw and treat the line profile as a Lorentzian whose width is aP where a is a constant for broadening of CO2 lines by air (there is some dependence on rotational state, some non-linear component, but remember this is back of the envelope)
The integral of the Lorentzian profile across all frequencies is unity (1). The total absorption of the line whether broadened or not will be Abs = A PCO2 L where A is the line absorption, PCO2 the partial pressure of CO2 and L the path length. PCO2 = VMR P where P is the total pressure and VMR is the volume mixing ratio.
At line center (substitute x = xo) into the Lorentzian formula the magnitude of the maximum is
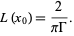The maximum absorption is Abs x L(xo). Substituting for Abs and Gamma we get
A is the integrated line absorbance for unit pressure, α the linear line broadening coefficient and VMR the volume mixing ratio.
If you go to very low pressures, the Doppler broadening approaches the pressure broadening and this approximation no longer works, but for tropospheric and stratospheric pressures it is fine.
Posts
6 comments:
Thanks Eli.
I take it when you say "A is the integrated line absorbance for unit pressure", you mean "per unit partial pressure CO2", right?
I found a paper that talks about the pressure broadening for Cesium, which comments that:
"As for the absorption coefficient, it should equal nLσ , where n is the number density, L is the path length, and σ is the integral of the absorption cross section ...Thus, the absorption coefficient should remain constant for a set of
scans at a fixed temperature but with different gas pressures..."
They use "number density" (of the cesium, in their case) instead of your "partial pressure", but at constant temp and volume they are directly proportional, of course.
I find it interesting that the width change of the Lorentzian is very close to linear over a fairly large pressure change (ie, that the line broadening coeff is actually linear).
Is this because the number of collisions per second is linearly related to the pressure and thus the fraction of the time any given CO2 molecule spends in the vicinity of another molecule (close enough to interact) also increases linearly with the pressure?
If this is true, I would expect that this linear relationship would no longer hold at very high pressures (ie, at very high pressure, one would no longer get much broadening with change in pressure). is this true?
Also interesting is the fact that there is a shift in the location of the line center with increasing pressure. I guess one would need to look at this at higher wavenumber resolution to see if SpectraCalc actually calculates this shift.
"that the line broadening coeff is actually linear)."
should read
"that the line broadening coeff is actually constant (that the relationship is linear).
The linear relationship between (collision-induced) line broadening and pressure change suggests that one can use line width to measure pressure.
I found this proposal to use that for a particular application.
Anon, as far as I remember it has been done but you need a very narrow band laser and fairly high pressure.
As a physical chemist from way back i think your explanation is spot on. Which leads me to the question of why do I see discussions (from those who should know better eg on RC) about the increase in total absorbance when broadening is included. Do you know if the current GCM's take it into account. My reading of AR4 seems to indicate not.
I think you have to be careful about differentiating between total absorption and total absorbance. In the absence of pressure broadening there will be very high absorbion and absorption over the very sharp spikes that constitute the spectrum. As pressure broadening spreads the absorbance over a wider wavelength range, filling the holes between the sharp lines the total absorption (in the sense of the amount of energy from a continuous source absorbed) increases and generally RC gets this right.
The answer to your second question is similarly complex. There are radiative transfer codes that take everything into account, e.g. LINEPAK, OTOH there are also simpler codes that fake it, like MODTRAN (see the online version), but which are calibrated against the more complex codes. The GCMs use versions of the simplified codes, but the costs are well understood and the benefit is that to go the whole hog would require to much time or too much computer. Of course, GCMs have to do a lot of other things at the same time. If there is a problem wrt radiation it has to do with aerosols and clouds, not gas phase spectroscopy.
Post a Comment