There Are Times That Try Bunny's Brains
This has lead to the suicide of as many physicists (Boltzmann and Ehrenfest among them) as Schroedinger's cat. Recently friends Motl and the Capitalist Imperialist Swine have wandered into the killing field. The Pig plays the chalk, quoting BoltzmannLoschmidt's paradox is that the laws of thermodynamics are time asymmetric because entropy always increases, but the underlying laws of physics are symmetric under time reversal. It should not therefore be possible to derive the second law of thermodynamics from first principles.
There are times in every blogger's life when a Bunny comes across something that is really really interesting, but does not have the angle or the understanding to really push to a conclusion. "A proof of Clausius' theorem for time reversible deterministic microscopic dynamics", Journal of Chemical Physics, 134 (2011) 204113 by D.J. Evans, S.R. Williams and D. J. Searles is the ticket for Eli. This trio has been thinking about how to establish thermodynamics on other than the normal ad hoc basis. Yes bunnies, the laws of thermodynamics are observations, better put Ansatze, or as the Wikipedia puts it educated guesses that are verified later by its results. The Clausius inequality, should the readers have forgotten isOf course, when the past is determined by the correct method – the method of retrodictions which is a form of Bayesian inference – we will find out that the lower-entropy states are exponentially favored. We won't be able to become certain about any property of the Universe in the past but some most universal facts such as the increasing entropy will of course follow from this Bayesian inference. In particular, the correctly "retrodicted past entropy" will more or less coincide with the "actual past" curve.The secret sauce is the statement that in retrodictions
...the lower-entropy states are exponentially favored.I'm putting that in my "remains to be demonstrated" file.
EW&S prove this is true only in the limit of infinite time, where the temperature is that of the "underlying equilibrium state" and only assuming T-mixing, ergodic consistency and the axiom of causality. That means, of course, that there are quantum issues yet to be confronted, but certainly this appears valid for classical thermodynamics.
In a later paper (JCP 137 (2012) 194109), the three authors conclude:
Our proof (of the zeroth law) is constructed using an array of previous results. Out proof of the zeroth "law" is far more informative than the corresponding derivation using ergodic theory. Combining the present proof with the observation that for an isolated mechanical system the energy is constant and our recent proof of the Clausius inequality, we see that all the so called laws of classical thermodynamics are mathematical results provable from the laws of mechanics supplemented by the axiom of causality and by the T mixing condition. Theis might be regarded as changing the logical status of thermodynamics.So why does the Gibbs approach to equilibrium work?
A second, less obvious result of our work is that for nonequilibrium systems entropy seems to play no role at all! Its place is taken by dissipation. The idea that one could use the Gibbs entropy in proving relaxation to equilibrium is obviously erroneous as discussed in a range of papers . . . . .
The present work points out, however, that entropy is not really necessary away from equilibrium. It is only at, or very near to, equilibrium when dissipation is identically zero or so small that local thermodynamic equilibrium can be assumed, that entropy (and the Gibbs approach-ER) may be useful. One may resort to other dynamical notions of entropy, cf. the Bolzmann entropy, or the one defined in the third paper of Ref. 21 to avoid these problems.The infinite time is where the fun lies. Remember Loschmidt? In a purely mechanical universe, motion is time reversible, e.g. given a complete description of the initial condition one can postdict where all the particles were at earlier time and predict where they will be in the future, but classical thermodynamics claims this not to be the case, and statistical mechanics establishes that for large systems this will not be possible because of entropic driving forces.
About a decade ago Evans and collaborators showed experimentally, that for small systems, easily of the size of today's nanostructures, there can be momentary violations of the second law. There would appear to be nothing really standing in the way of building an entangled system of such a size and that could really be the Mayan calendar for physics.

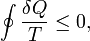




32 comments:
Predicting where things will be in the future is one thing, but if the things in question are posessed of volition, one cannot know what they will be doing there, even if they are entangled.
Is there such a thing as volition in a mechanical universe? Escape to religious belief is also fraught with questions. Down that path goes only Willard, and unwillingly at that.
I thought the basic issue with the second law was that it requires the universe to have begun in a highly non-equilibrium state as a whole, so that it can gradually progress to equilibrium over long-enough periods of time for interesting stuff to happen. Roger Penrose has discussed this at length, I think I ran into it in his book "The Nature of Reality". It's central to his argument against Inflationary cosmology which requires an even higher level of unlikeliness in starting conditions.
Hey, I follow this blog for climate-related stuff, not physics. Anyway, it's somehow reassuring to see Motl is just as obnoxious on ergodic theory as he is on AGW.
On the topic at hand, I've found the "Kac ring" model a good elucidator.
Rab, how could a bunny forget the Kramm lectures on the second law from years ago?
Kramm lectures?
If there isn't a link to youtube, I'll have to assume that they never happened. ;)
Of course there's such a thing as volition. There's just no need to posit that to non-biological processes.
Willard Tony's determination is not that determined.
Speaking of which, let's recall that photo-documentary:
http://witsendnj.blogspot.ca/2011/07/beware-banality-of-evil-heartless-at.html
Here, in the comments among other places
Good times:)
This reminds me the time Gerhard went to town against your comments at Susann's:
> Sorry, my time is too valuable to response to [Eli]’s “bla bla blubber”.
http://metaclimate.org/2012/04/14/arguing-with-stupid-people/#comment-6841
Ah, the good ol' days.
"argument against Inflationary cosmology which requires an even higher level of unlikeliness in starting conditions."
"Real physicists" don't worry about how the early universe happened to start out in an incredibly highly ordered (and hence highly improbable) state.
After all, it's nothing that the multiverse can't "explain".
~@:>
For more amusement of the greenhouse effect second-law-violation variety check out the comments to Roy Spencer's latest attempt to remind people he's actually a scientist at heart:
http://www.drroyspencer.com/2013/01/misunderstood-basic-concepts-and-the-greenhouse-effect/
The second law explained:
Consider a perfect billard ball rolling over a perfect pool table which is perfectly circular.
"Physics obviously doesn't contain any inconsistencies." -- Lubos Motl
Just infinities...which are consistently swept under the rug or renormalized away.
But String theory(s) will fix all that, right?
~@:>
No teleology intended, Eli-- it's easy to program a Turing machine whose next output is unknowable, and presumabbly just as easy to entangle two, but ifwe were to entangle two of you, one might be as ornery as the other
...the early universe happened to start out in an incredibly highly ordered (and hence highly improbable) state.
That one again? Who ever started it? I've heard no evidence that the earliest universe was not just about as disordered as it could be for it's size.
Pete Dunkelberg
I thought the basic issue with the second law was that it requires the universe to have begun in a highly non-equilibrium state as a whole,....
Well, it did. I don't know about thermal non-equlibrium though. Later on, local heat sources aka stars happened.
Pete Dunkelberg
Eli: This trio has been thinking about how to establish thermodynamics on other than the normal ad hoc basis. Yes bunnies, the laws of thermodynamics are observations, better put Ansatze, or as the Wikipedia puts it educated guesses that are verified later by its results.
What then are Newton's laws? But in both cases the testing has been as thorough as we could make it, and in such diverse settings that it is far far beyond mere curve fitting. The "problem" is that for historical reasons some want to derive all later science from Newton. But the 2nd law of thermo seems to be an emergent (read: hard to derive) property of many-particle systems. Might this also be true of Newton's laws vis-a-vie quantum particles? This has been suggested by physicist Robert Laughlin. Anyway the dream of derivations all the way down is doomed to remain a dream. For consolation though, try to derive Newton from Clausius.
Pete Dunkelberg
Pete,
The available evidence indicates a highly uniform distribution of matter in the early universe, which (though it might seem counter-intuitive) is an extremely ordered state (very low entropy) in the presence of gravity, which acts to lump stuff together.
I don't think there are many cosmologists who doubt that.
~@:>
Damned cosmologists, always starting rumors (and then hiding in black holes to cover their tracks.)
~@:>
"Atoms Reach Record Temperature, Colder than Absolute Zero"
http://www.livescience.com/25959-atoms-colder-than-absolute-zero.html
Say goodby to the second law.
@David B. Benson:
That is an execrablel title. As the body of the article explains, so-called "negative temperature" systems are not "colder than absolute zero", they are "infinitely hot". "Negative temperatures" - an idea that goes back to Ed Purcell and Norman Ramsey in the 1950's - are used to describe systems with inverted populations (more molecules in higher energy states), such as occur routinely in NMR and laser physics. That's what the formalism was invented for. This latest development involves applying these to translational degrees of freedom - a really cool experiment, but not a fundamenally new concept. The laws of thermodynamics are not violated, as long as you express them carefully (as Ramsey did in his analysis.) You still can't make a perpetual motion machine. You can't win, you can't break even, and you have to play.
rp^2 --- At least the title is not execrable.
:-)
Ah but in the spirit of Evans. Williams and Searles, if you have to play against the house shove it all in on one bet on red.
> Evans ...
"... over periods of time less than two seconds, variations in the random thermal motion of water molecules occasionally gave individual beads a kick. This increased the beads' kinetic energy by a small but significant amount, in apparent violation of the second law.
The gain is short-lived ...."
---
So is this not analogous to how greenhouse gases accept a kick from random motion and occasionaly get wound up, spun up, twisted up, or otherwise irritated enough to emit a photon?
I keeps thinkin', we need little teeny floaty nano-sized Brownian-pumped or solar-pumped (or HAARP-pumped, I suppose) or just Maxwell-demon-ratchet-equipped stratospheric infrared laser molecules that know which way is up, and emit those infrared photons not randomly but biased _away_ from the planet ...
If you only look at one collision between two molecules it is exactly equivalent, however if you look across a large number of collisions and molecules you get a Boltzmann distribution.
However, to extract useful energy from the process you need an array of Maxwell's demons.
Anon - well yes but there is quite a difference, entropy wise and otherwise, between evenly distributed as points on a grid and as madly dashing particles of a hot gas. Inflationary cosmology (IC) first starts with a very small volume such that thermal equilibrium is the case, and then leads to the distribution of matter that is observed. I see from Wikipedia on IC that Penrose has different ideas on the subject. I have not read his Road. Doubtless this marks a distinction between me and at least one other commenter. Years ago I read a popular book by Penrose, partly to learn about his ideas on "quantum consciousness". The latter seems to have two problems: the quantum part doesn't work (decoherence is too fast by a very large factor) and if it did (and overlooking the other differences this would make in our world) the relationship to consciousness is obscure. This may be related to another difference between me and a commenter or two: I don't take Penrose too seriously. ;)
Pete Dunkelberg
Eli, have you looked at Evans and Searles' Fluctuation Theorem in Advances in Physics? That seems to be where they define their "dissipation". I am trying to understand just what that might be related to physically in the system and how it would relate to entropy. Any clues?
Pete,
Physicist Brian Greene sums up the issue (in Fabric of the Cosmos. pp173-174) thus:
"The ultimate source of order, of low entropy, must be the big bang itself. In its earliest moments, rather than being filled with gargantuan containers of entropy such as black holes, as we would expect from probabilistic considerations, for some reason the nascent universe was filled with a hot, uniform, gaseous mixture of hydrogen and helium. Although this configuration has high entropy when densities are so low that we can ignore gravity, the situation is otherwise when gravity can't be ignored; then, such a uniform gas has extremely low entropy. In comparison with black holes, the diffuse, nearly uniform gas was in an extraordinarily low-entropy state."
If you have an issue with that description, you'll probably have to take it up with cosmologists (and not just Roger Penrose)
~@:>
Please not with Roger Penrose.
Not on Eli's blog.
Please.
david,
It's unclear why Pete brought up Penrose, anyway.
The claim of a "highly uniform distribution of matter" in the early universe (which necessarily implies "highly ordered", and "low entropy" when gravity is present) is based on very strong evidence -- eg, the high degree of (though not perfect) uniformity of the temperature of cosmic microwave background radiation.
The claim rises far above the level of "speculation" (or "internet rumor"), by Penrose or anyone else.
But, like so many "discussions" of science on blogs, this one seems to have left the beaten path and is now headed off into the dense thickets.
C'est la blog.
~@:>
Changes in mean molecular gravitational potential energy affect entropy. Hence the Clausius statement is only always correct in a horizontal plane in a gravitational force field. The HUGE significance of this is that it smashes the greenhouse radiative forcing fictitious, fiddled physics, as explained here where there's a few thousand dollars for the first to prove it wrong.
Time for a new Doug Cotton filter.
Post a Comment