All functions belong to the firm of Mclaren Maclaurin and Taylor in the short term
See UPDATE BELOW and FURTHER UPDATE
Further UPDATE: His original mistake has cost Eli no end of aggro, coupled with more than a bit of chocolate flung his way by Msr. Pielke, however, being a thinking bunny, he has gone back and thought. What we all have missed, and what explains the results in the chart below is that the Maclaurin series is a power series expansion around a point where the function and its derivatives are evaluated at a not constantly changing. This continues at the return of Maclaurin and Taylor. In the end, using a linear approximation within the range of temperature found on Earth is perfectly reasonable no matter what the Old Guy says
where the function and its derivatives are evaluated at a not constantly changing. This continues at the return of Maclaurin and Taylor. In the end, using a linear approximation within the range of temperature found on Earth is perfectly reasonable no matter what the Old Guy says
Ethon flew back from Boulder where he had been keeping company with the math department while Roger Pielke Sr. was retaking Cal I. To tell the truth the JGR D editors could use a refresher too. Atmoz first pointed Eli to this, so when Eth came flying in Rabett Labs was up and running. Were Eli a cynical Brit he would think the old Guy might be the only person trying to enter the IPCC with honourable intentions:
which he elaborates in the comments at Atmoz (At does a pretty good job of demolishing this himself)The definition of the global average surface temperature used by the IPCC and others can be expressed as
dH/dt = f -T’/λ
where H is the heat content of the land-ocean-atmosphere system, f is the radiative forcing (i.e. the radiative imbalance), T’ is the change global average surface temperature in response to the change in H, and λ is called the “climate feedback” parameter which defines the rate at which the climate system returns forcing to space as infrared radiation and/or as changes in reflected solar radiation (such as from changes in clouds, sea ice, snow, vegetation, etc).
There is a fundamental problems, however, with the use of this equation for the description for global warming.
T is defined in the above equation as a global proxy for the thermodynamic state of the climate system. As such, it must be tightly coupled to that thermodynamic state of the climate system. Specifically, in this context, T is the global average radiative temperature of the Earth’s surface since the outgoing radiative flux at the top of the atmosphere is determined to a large extent by the surface radiative temperature. However, this outgoing longwave radiation is proportional to the fourth power of T. T’ = +1 C in the polar latitudes in the winter, for example, would have much less of an effect on the change of longwave emission than T’=+1°C increase in the tropics. The spatial distribution of T’ matters, whereas the equation given above ignores the consequences of spatially varying values of T’.
Eli pointed out that since Maclauren and Taylor tell us something moreTo assess the use of the global average of [T**4 - (T+T’)**4], the spatial map of this field should be presented. This would show where the change to the value of sigma T**4 is the largest. Please show this. The plot of “normal” and ‘average” radiative temperature is not what we are proposing.
Indeed, it is easy to show that weighting by (T+T’)**4 significantly emphasizes the lower latitudes, since the relationship is to the 4th power of temperature. I look forward to your analysis as we have recommended.
(T+T’)^4 = T^4*(1+T’/T)^4
assuming T’<<>
(1+T’/T)^4 ~ 1 + 4 T’/T+ higher order smaller terms, and then
[T**4 - (T+T’)**4] = 4 T’
UPDATE 2/6/08: As pointed out in the comments Eli screwed this up
[T^4 - (T+T’)^4] = T^4-T^4*(1 + 4 T’/T) = T^4* 4 T’/T= 4T'*T^3
good thing no one reads this blog. The change in emission depends on T^3 for a constant change T'. OTOH for the 250-350 K interval this is also pretty well approximated by a linear function in T.so as long as T’ is small compared to T (1K/300K is pretty small) the change in radiation is linear in T’ EVERYWHERE so Roger’s ”
“Indeed, it is easy to show that weighting by (T+T’)**4 significantly emphasizes the lower latitudes, since the relationship is to the 4th power of temperature. I look forward to your analysis as we have recommended.”
is just wrong, as anyone who learned about series expansions of functions in Cal I would know. Given the back and forth with Roger Pielke Jr. about Hansen's 1988 scenarios being exponential or linear, this failing appears to be genetic.
Above, Eli has shown that the CHANGE, in blackbody emission for a body at any temperature T by a small amount T' is linear in the change in temperature. This means that if you are looking at changes in emission due to changes in temperature, it doesn't much matter if you take it as functions of T'^4 power or T'.
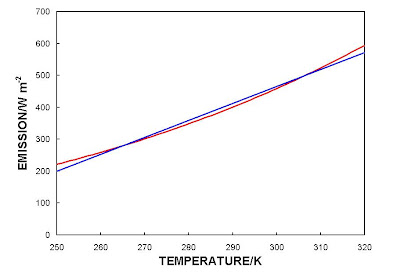
Yet, young bunnies, lets see how well a linear form fits the Stefan-Boltzmann curve itself over a reasonable temperature range of 250 to 320 K (-23 to +47 C, ethical science bunnies don't do no F).
The red line (the red S-B curve) fit's pretty well to a linear function of temperature (the straight line). Tant pis Roger.





56 comments:
This is totally off topic, but I have come to the conclusion that I am dumb.
For the life of me, I do not understand the cooling stratosphere (other than what is caused by ozone depletion). Which means I don't understand radiative physics. I thought I understood it well enough, but It's clear that I don't understand it at all.
I have read what's on Realclimate and I have read Eli's explanation and I have read William Connelley's description and I have read http://www.atmosphere.mpg.de/enid/20c.html. Still don't get it.
There is virtually nothing in AR4, other than to say, "it's cooling."
So, back when I thought I was smart, I said, "Because of the enhanced greenhouse effect, less long wave radiation is escaping to the stratosphere until equilibrium is restored, thus it is cooling."
But that is apparently wrong. I read things like, "In the stratosphere this emission of heat becomes larger than the energy received from below by absorption and, as a result, there is a net energy loss from the stratosphere and a resulting cooling." And here is where I am dumb. 1) How is it physically possible to emit more than it abosrbs and 2) Why does any of this matter anyway? Why would the presence of more CO2 cool the stratosphere when the alternative for the LW radiation is an essentially unobstructed path straight to outerspace?
You don't need Taylor/Maclaurin for this.
(T+dT)^4 = T^4 + 4T^3dT + 6T^2dT^2 + 4TdT^3 + dT^4.
Neglecting dT^2 and above, (T+dT)^4 -T^4 = 4T^3dT
The equators might be at 300K, the poles at 250K (very roughly speaking). So the 4T^3 coefficient here will differ by about 70%. Whoop-de-doo.
cce, you are not alone, I don't get it either. I thought what was supposed to happen was the troposphere was supposed to warm faster than the surface. People say this is wrong, and what is supposed to happen is not that at all (though I can't see why not) and that the strat is supposed to cool, and I cannot either see why it should.
anon1132
Maybe our physicist host can explain it to us. I really would like to understand this.
Ignorance is not scepticism or denialism by the way. Its genuinely not understanding, as when one does not grasp how to do arrays in Python, which is not a statement that one does not believe Python does arrays, just a confession that right this moment he don't see how to make it.
Here is my take on the stratosphere temperature. Below the tropospause the atmosphere is to a large extent heated by convection from the surface, above the tropopause you have a temperature inversion and no convection, and the reason for this is that this layer is heated by solar UV. This heating will not change if you add more CO2, but with more CO2 the atmosphere becomes more efficient at emitting IR. Since you can't emit more than you absorb the temperature has to drop. (The added CO2 does absorb a little extra IR from below, but not enough to compensate). You can't explain either the existence of a stratosphere or why it should cool without taking into account heating from UV absorption.
The troposphere is indeed supposed to warm faster than the surface due to water vapor. The wet adiabatic lapse rate drops with temperature.
The equ RP uses isn't the defn of temperature.
Re the strat: I think TP is largely correct. One consequence is that if you had a grey atmosphere (no ozone etc) then the entire atmos warms under GW. Ie, the cooling predicted there isn't because of the height, or because its the top, but because of an "accident" of its structure.
I've never seen a good simple authoritative explanation of this. My expl is good and simple but not authoritative :-)
Good post. However, the line "assuming T’>>T you get" has the inequality backwards - thanks!
The line "assuming T <<>"
still looks like a typo to me - I guess it means to say:
assuming T' << T
Thomas,
Thanks for the description. But my problems are more basic.
If CO2 is the only thing in the statosphere that can absorb LW (however scarce it may be), then it's the only thing that could possibly delay its trip to outerspace. If there was no CO2, then there would be no absorption and thus no delay.
I know that this is totally wrong, but it's only the result of my totally wrong understanding of physics.
In addition to CO2, there is also ozone in the stratosphere which can absorb long wavelength radiation, also minor traces of other greenhouse gases.
However, for general purposes, the density (read pressure) in the strat is too low to intercept more than a small fraction of any outgoing long wavelength radiation that happens to be at a wavelength that can be absorbed, besides which almost all the blocking occurs in the troposphere.
My question is, why would it matter if there is more CO2 in the stratosphere? If it can't emit what it doesn't absorb it is doing nothing. And even if it is absorbing a tiny amount, that means at least some LW radiation is being delayed on its way toward outerspace, and more CO2 would mean more delay and thus more warming.
I am missing something fundamental.
Well I admit to fairly thorough confusion, but thought it went something like this.
The CO2 and the other GGs absorb radiation and thus heat up. Because there is none in the stratosphere, this does not heat up. So the result is, the trop gets warm and the strat don't. The trop is warming by radiation from the surface. Why this should cause the strat to cool though?
Now something happens which I don't grasp. The trop warms from this upward radiation. As it does so it slows the rate of heat loss from the surface. This seems understandable. The surface thus warms. But for some reason, the resulting radiation from the surface causes the trop to warm faster than the surface, while remaining a lot cooler than it in absolute terms? Why?
Is this right, or if not, what?
anon1132
Didn't we go through all this before?
The reason why the stratosphere cools has nothing to do with ozone (remember the mesosphere is cooling too). Instead it is related to the spectral nature of the absorption and the fact that CO2 is a much larger component of the emitters above the tropopause.
With increased CO2, there is more blocking at the key lines (15 um) in the troposphere. There is a matching increase at other lines. In the stratosphere, there is absorption and emission at 15 um as well. And at that line (which is more dominant a part of the IR there than below), the absorption from below will be less, but the emission will be more. Thus a cooling.
Gavin,
Thanks for the explanation. However, it is the one I started with (which I don't understand).
Maybe this will work: Perhaps someone could describe it in terms of the voyage of a single infra-red photon. What is the voyage like with "normal" amounts of CO2 in the stratosphere. And what is it like with elevated amounts of CO2 in the stratosphere, keeping all other variables the same? The only change would be an instantaneous increase of stratospheric CO2.
Put another way, if an animator was going to draw a cartoon of infra-red radiation leaving the earth under those two cases, what would you tell him/her?
Since RP Sr, it seems, still does not invite comments "over there", and since after almost a week he has not replied to your (Chief Rabett's) comment over at Atmoz, and knowing he occasionally keeps an eye in over here, when do you think he might be popping by here to reply on this point?
I'd like to see how this develops.
Cymraeg llygoden
PS I know you're constrained in the blog format and that you're trying to make it easier for the reader, but I hope the recent red and blue outbreak is not used too much. I'd hate to think it was taking on the appearance of a Piers Corbyn fiasco ... sorry, I meant forecast. (Long way to go on that score, I know.)
PPS Given the recent very long blogs and, no doubt, increased comment traffic, it's getting difficult to know what has recently been commented on without doing lots of scrolling/digging through pages. Is it possible to work in something like a "recent comments" box (between the ads, maybe)?
Nick barnes said: "The equators might be at 300K, the poles at 250K (very roughly speaking). So the 4T^3 coefficient here will differ by about 70%. Whoop-de-doo.'"
Actually, if you are talking about a 50k change from about 300K, that's starting to deviate significantly enough that you really should not use the differential -- (4T^3)dT -- approximation for the change.
The radiative emission for a black body at 300K is 2.1X what it is at 250K (ie, 110% higher instead of 67%)
The radiative emission for a black body at 300K is about 1.4X what it is at 275K (ie, 40% higher)
For those who would claim that a 110% (or even 40%) change in radiative emission is insignificant, I'd simply have to disagree.
--T
T--
What Eli was saying is that you can fit the dependence on T with a linear function fairly well over that range (see graph) so keeping track of T rather than T^4 makes sense. BTW note that the straight line fit does not go thru the origen
Hey Rabett, going off topic again, every man and his dog is running with the achievement of 13m sq km area of Arctic ice. Most unfair, as you, Shirley and I were right up with this story months ago. 10m sq km "unprecedented" ice return- how has old Gaia done it?
Brrrr type cold all around the Arctic so plenty of ice still to grow.
JohnS
You're skating on very thin ice there Johnny darlin.
There is more than one thing at play in the stratospheric cooling. The spectral decomposition of absorption vs. emission Gavin mentioned is definitely important -- namely the fact that the stratosphere emits well in the CO2 band, but the upwelling IR is depleted in this band, so that increasing CO2 has a disproportionate effect on cooling. However, even for a grey gas there is a stratospheric cooling in response to GHG increase, if there is solar absorption (think ozone) in the stratosphere. The reason is that a big part of the stratospheric balance is heating by solar absorption vs. IR cooling. Increase the GHG and you get more cooling (at a given temperature) balancing the same solar heating, hence the stratosphere can get cooler.
For the more mathematically inclined, Chapter 4 of my book has an analytic grey gas solution of radiative equilibrium with solar absorption, which illustrates this point. Needs calculus, but nothing more.
I wonder if this is another one of those cases where the paper itself said something a lot less outrageously wrong than the spin put out by the author's blog. I'd hate to think GRL could let something this bad slip through, but it wouldn't be the first time.
I suppose I should go take a look at the original It's on the queue.
I think I get it better now with both Raypierre and Gavin's explanations combined. This was one big hurdle for me to conceive in relatively accessible terms. That page had helped me a lot, however:
http://www.atmosphere.mpg.de/enid/2__Ozone/-_Cooling_nd.html
Question for Raypierre: The (nice) Iacono and Clough graphic representation is from 1995, is is still widely accepted as pretty much valid?
Saturnian.
The statement that
[T**4 - (T+T’)**4] = 4 T’
so as long as T’ is small compared to T (1K/300K is pretty small)
is not correct.
If T' is small compared to T, the change in emission is essentially equal to the differential of sigmaT^4, which is proportional to both T' AND T^3
In other words, it should read
[T**4 - (T+T’)**4] = 4T'T^3
When going from the pole to the equator, T^3 changes by roughly a factor of 1.7 (if one assumes the respective temps are 250K and 300K)
(I believe this is what Nick referred to above when he said 70% change. Sorry for the earlier misunderstanding, Nick)
So, the change in emission for a 1K change in temp at the equator is 1.7X what it would be at the pole.
Is that significant?
Others are free to disagree, but I would consider it so.
--T
T: yes, that is what I meant.
anonynous at 7:47 AM has it right, I think. The RHS of Eli's first equation has the T^4 part factored out. This factor got dropped from his third equation.
maybe?
You are right and I was wrong. See update/
I guess this is what is called an embarrassed silence.
JohnS
Anyway Rabett, now that this little faux par is over(and I know you and your little mice here would be just as forgiving of SteveM if he made a similiar mistake over at CA- indeed the same magnanimity you show to the Pielkes in above), lets get back to the thin ice in the Arctic.
JohnS
Makes yah little worried that old Gavin and Raypierre didn't pick up this little error. These fellows telling us the world is coming to an end and all with their mathematical models.
JohnS
Its "pas" (as in step) not "par"
Thanks for correcting the mistake, Eli.
--T
PS JohnS?
Shut the f..k up. No one wants to read your BS.
It's good that somebody corrected the algebra error in Eli's exposition, but please don't lose sight of the fact that Eli's main point is correct. Over the range of Earth's surface temperature, little error is made by linearizing Stefan-Boltzman. Energy balance models do this all the time. Actually, the situation is even better than Eli represents, since the energy budget isn't actually determined by straight S-B, but by the OLR taking into account the vertical temperature profile, water vapor, and CO2. The water vapor feedback actually cancels out some of the curvature over this temperature range, making the linear fit even better.
But there's even a stronger reason that Pielke's claim is ridiculous. He says that because (as he claims) the OLR changes are proportional to the fourth power of temperature, using a linear temperature average "overestimates global warming." What the heck is that supposed to mean? That confuses the metric used to summarize global climate change (an average temperature) with the kind of model used to interpret that change.
And if you're talking about modeling, you need to remember that GCM's do not linearize Stefan Boltzmann. When they calculate the radiative transfer, they use the full form of the Planck function.
So, I'd say that even if Pielke Sr. were right about linearization errors (which he isn't), his claim about the average of T "overestimating" global warming is incoherent.
Eli makes a mistake, fesses up, and corrects. So how can it be an embarrassed silence? If Eli hadn't done anything to correct, then yes it would have been. And he also corrected himself at Atmoz.
Moreover, the algebra error (and there were a lot of T^4s etc. to sort out) was easy to overlook on screen. Indeed, I did so on first read through. It was only after --T replied to Nick Barnes that I went through it critically with pen and paper myself (kudos to them for being vigilant -- a timely reminder to all) and came to their same conclusion.
What Eli is guilty of (and we've all done it) is knowing the endpoint (the plot) and taking the wrong mental path there.
It's not about making mistakes (we all do), it's about how you go about rectifying them.
And anyway, is it not whether the plot is correct or not that is the main issue? Plugging some reasonable values into OOCalc seemed to me to confirm Eli's final-line analysis (i.e. the plot) of what needed to be monitored (because having tripped up on the algebra, I thought I'd best ...). Try it JohnS.
I'm surprised you didn't pick him up on "McClaurin" though. Oh hell! More Tippex required.
Cymraeg llygoden
Hey boys and girls, the wagons come a circle forming all around guru Rabett. Rabett wanted to be a little smarty pants, to pique the Pielkes, and made a booboo.
When SteveM made some errors last month, old Rabett and friends well piled in.
A little bit of humbleness, hey.
While on the misspelling, old cym, Rabett, about ten or so posts up, has origin as origen. Since you and belette seem to enjoy the waft of tippex, splash a bit more around.
JohnS
John S enlighten me and quote or link when StevMac admitted being wrong, so I can read the extent of his graciousness.
Saturnian.
The reference to the misspelling was really to highlight the inconsequentiality of your particular comments. Perhaps it was too obscure a point for some.
The red line (the red S-B curve) fit's pretty well to a linear function of temperature (the straight line). Tant pis JohnS.
Cymraeg llygoden
Hey Saturian, I thought you weren't going to ever ever to talk to me again.Go on, sunshine, admit it, you can't get enough of me. The mojo, itsa flowing agin hey Saturian
You old poseur cym, you get to smell the tippex while pretending it was a joke. The inconsequential in all this cym, is you thinking red line/blue line, booboo in maths makes a bit of a difference. Rabett makes a mistake and I'm the only fool to come charging in. SteveM makes a mistake and a cast of thousands comes charging in.
SteveM wins hands down as the person of consequence. I'm sure you will be able to dredge up some little pithy pis comment here, cym, makes you sound very exotic but faintly amusing.
JohnS
JohnS said of himself: "I'm the only fool to come charging in".
Well, your self-importance knows no bounds it seems, JohnS. As, so it seems, does your ignorance quotient and/or your inability to read and digest.
FYI, nick barnes and --T dropped in questioning Eli's algebra long before you raised your mug above the tesselations (unless you claim either or both of their identities of course). Follow the time line (something your alter ego is not too clever at sometimes, it seems).
By following the time line you will also note that nick barnes raised the spelling of McClaurin (indirectly) long before I did. Why I raised it is why I said I raised it. You just weren't paying attention, were you [he said rhetorically]?
A dunderhead espousing flummadiddle = JohnS.
Now there's an algebraic expression! If someone would just like to check my working out for me, I'd be grateful.
There may of course be equally correct alternative solutions here:
Glug! Shi... glug! Thought it was thicker than that. Splutter! = JohnS
is another possible solution that comes to mind.
Cymraeg llygoden
JohnS says Rabett makes a mistake and I'm the only fool to come charging in. SteveM makes a mistake and a cast of thousands comes charging in.
You got one thing right and it's not your second sentence.
Rabett's mistake was not central to his argument. It was tangential.
Steve McIntyre's mistaken claim regarding which scenario Hansen considered "most plausible" (ie, his claim that Hansen never said in his original paper that he considered scenario B "most plausible") was central to McIntyre's argument.
When Eli acknowledged and fixed the mistake, it made no difference to his argument that RPSr was making a big doo-doo about nothing. As Raypierre explained (thanks), the models actually use the full (sigmaT^4) version of SB equation so even if Pielke happened to be right (which he is not) the argument Pielke is making would still be moot. (Pielke does not even seem to understand what the mean global temperature anomaly is. Hint: that first equation with the lambda and H is not how it is calculated)
...and when Eli made the correction, he left the original in place so people could see what the error was.
When McIntyre "fixed" (ie, erased) his "error", he basically made his (McIntyre's) entire argument moot.
He also let all of us know that he had never read the original paper -- at least not in any detail because Hansen's statement that he considered scenario B "most plausible' was plain as day to anyone who cared to look. ( Thanks Steve M. for letting us know what a fine auditor you are!)
Finally, the fact that McIntyre made the change without leaving the original text in place basically says it all.
--T
Whoops! I meant crenellations above, not tessellations.
(I'd just finished reading about tessellating a plane with triangles when I wrote the above. Doh!)
Cymraeg llygoden
Eli--
Didn't Roger Sr.s point about overweighting have to do the percentage errors?
So.... to find out how much of an error the T' makes as a fraction of the amount radiated, divide by T^4.
To leading order, the error expressed as a fraction of the energy leaving is... ta... ta... ta... da...
4 T' T^3/ T^4 =
4 T'/T
That is: Small. Very small. And, better yet, since this is a fraction, dimensionless. :)
The same issue of T^4 came up elsewhere, where somehow the whole T^4 thing was supposed to explain away the whole usual 33K greenhouse increment expected based on the simple zero-d models for a constant temperature planet.
I wrote a post showing the T^4 issue can't be used to erase the need for the basic greenhouse effect.
The T^4 issue doesn't matter much when defining some sort of average climate temperature.
If Roger Sr. larger point is he wants to measure enthalpy in the dH/dt term, he should worry about the heat of fusion when ice melts or latent heat when water evaporates.
Who knows, maybe that matters? However, if it does it would mean mean dT/dt underestimates the enthalpy change for the climate.
"The T^4 issue doesn't matter much when defining some sort of average climate temperature. "
Doesn't even enter into it, unless you are Roger Pielke or Ross McKitrick.
Global mean temp anomaly is defined (by NASA and most other climate scientists) as an arithmetic average for a reason: because T is what we measure with our thermometers (!) and it is T, not T^4, that is a measure of average translational kinetic energy of molecules in a parcel of gas (and hence a measure of the translational energy content of that parcel).
When the translational energy content changes, it is temp anomaly that is a gauge of that change ΔT, not ΔT^4).
--T^4
Note: McKitrick, uses C^4 (ie, Celsius) rather than K^4 (kelvin), which makes the whole T^4 argument even more ridiculous in his case.
lucia says:
"To leading order, the error expressed as a fraction of the energy leaving is... ta... ta... ta... da...
4 T' T^3/ T^4 =
4 T'/T
That is: Small. Very small. And, better yet, since this is a fraction, dimensionless. :)
Is that a surprise?
When you made the assumption that the change in emission associated with the temperature change was proportional to T'T^3, you implicitly assumed that the temp change T' was small compared to the starting temp (ie, that T'/T << 1), so it should come as no surprise that the fraction you get in the end (change in emission over original emission) is also very small. In fact, if it were not, using the differential approximation would not have been warranted. :)
anonymous--
Of course it's not a surprise.
I'm simply pointing out that Roger Sr. was discussing impact as a fraction. Eli discussed absolute without dividing for the average.
Dividing by the average to illustrate the % difference-- connects Eli's comment to Roger Sr.'s actual claim shows Eli is more correct.
In fact, I'm pretty sure we were to look at the specific issue if spacial variations Roger Sr. alluded too, it's easy to show that the thing Roger Sr. is worried about only contributes to (T'/T)^2.
The square comes out due to the properties of averaging. If Eli is interested, I can show that tomorrow.
Lucia: Eli discussed absolute without dividing for the average.
If one is concerned with global average temperature anomaly (ie, change), isn't it precisely the absolute (rather than the fractional/percentage) changes across the globe that are the relevant thing?
Lucia: The square comes out due to the properties of averaging.
I, for one, am very interested in seeing how "squares" can be involved with arithmetic averaging of temperature (which is used to get the global mean temp anomaly) :)
--T^4
Anon.
f one is concerned with global average temperature anomaly (ie, change), isn't it precisely the absolute (rather than the fractional/percentage) changes across the globe that are the relevant thing?
Not really. Eli is commenting on Roger Sr.'s post, comment at Atmos and published paper. I at least think Roger is discussing fractional errors-- that is whether the stuff left off is small compared to the stuff retained in the equation.
I think (and hope) that Roger Sr. does understand and accept that approximations are sometimes made. So, the issue is: Is the amount ignored 1% of what's kept? 10%? 200% etc.
On the next bit, interesting snipping of the words around what I actually said. :)
The square term is the leading order term in the error in using the
dH/dt = F - T'/λ (1)
approximation for the planet due to the in the temperature difference between the poles and the equator.
It's this temperature variation Roger Sr. seems to think invalidates the use of that equation by the IPCC.
And guess what-- the reason the error is quadratic, is precisely because the average used to get the anomalie is an area average. :)
lucia: "So, the issue is: Is the amount ignored 1% of what's kept? 10%? 200% etc.'
Thanks for pointing out the "issue" to all of us.
Some of us had no idea that this had anything to do with approximation.
--T
PS: I was one of the ones who noted the error in Eli's approximation equation. :)
Anon--
I'm assuming if you knew this wsa the issue was the % error, then you are not hte Anon who later suggested the % error was not the issue, and whom I answered?
Of course, in my answer to the suggestion that the % error was not the issue, I said the % error was the issue.
When I answered, I did not wish to suggest no one here knew the issue was the %error. I guess I could have waited for you, anon to tell the other anon the % error was, indeed, the issue?
(Or if you are the same anon, let you realize that you are alternately changing your mind and posting?)
Lucia: "I'm assuming if you knew this wsa the issue was the % error, then you are not hte Anon who later suggested the % error was not the issue, and whom I answered?"
No, it was me (T) in both cases.
And it is you who are confused.
Though percentage (or fractional) error is obviously an important consideration when deciding whether a "small approximation" is valid, percentages (ie, fractions) T'/T ARE NOT what one uses to CALCULATE global mean temp anomaly. One uses actual temperature changes (from some baseline) for that.
Most importantly, you are basically arguing about something here that, as Raymond Pierrehumbert points out above, really turns out to be a non-issue in this case, since the climate models do not make the linear approximation (they use the full Stefan Bolztmann) and RP is basically confusing a model with the metric (global mean temp anomaly).
You really should read what Raymond Pierrehumbert said above because he summed up quite nicely what the real problem with RP's argument is:
But there's even a stronger reason that Pielke's claim is ridiculous. He says that because (as he claims) the OLR changes are proportional to the fourth power of temperature, using a linear temperature average "overestimates global warming." What the heck is that supposed to mean? That confuses the metric used to summarize global climate change (an average temperature) with the kind of model used to interpret that change." -- raypierre
Finally, I suggest you look at how NASA actually calculates global mean temp anomaly. It does not involve T^4 in any way shape or form.
--T
PS: I suggest you cut the rhetorical games to score debating points. it adds nothing of any substance to the conversation. (and reminds me of RPjr :) )
As a coauthor of the Pielke Sr et al. JGR paper (I was far down the coauthor list but contributed directly to the quoted section) and having just stumbled upon this thread, here are semiofficial comments.
There's no calculus error in the quoted text. JGR's editors (and reviewers) need no refresher course.
Pielke Sr' calculus error (weight by T^4) is smaller than Eli's calculus error (weight by T^0), given that the correct weighting is prop to T^3, as noted and corrected. I clean up my office about once every five years, so, if challenged, I can probably recover the piece of paper on which I jotted down 4T^3 while working on the manuscript.
The resulting difference in emission change, however you slice it, between similar temperature changes at pole and equator is quite a bit beyond the negligible 10% level, and that's why we thought it worth pointing out in our paper.
Eli's plot of emission vs. temperature encourages the reader to intuit that the error is somehow proportional to the difference between the two lines. It's not...it's proportional to the difference in slope. Differentiate, and it will be readily apparent that the derivative (change in emission vs. change in T) changes by a few tens of percent over the plausible temperature range.
Lucia's mention of the smallness of (local change of emission)/(local emission) is akin to arguing that global warming is not a problem because the radiative imbalance is only a tiny fraction of the total radiation received or emitted.
The issue of T vs T^4 is pretty minor, though, impacting subtle problems in climate response and sensitivity when there are bigger issues to sort out at the moment. When we brought it up in our paper, we only gave it one paragraph of space and not even a passing mention in the abstract.
I should add that I take no responsibility for anything Roger Pielke Sr. says that's not contained in a coauthored paper.
John - I also add that I take no responsibility for anything that you have written that's not contained in our coauthored paper; a paper which you 100% agreed with. :-)
I will be weblogging in a few days on the subject of this thread on Climate Science. It is remarkable that several of you have missed such an obvious error and continue to perpetuate it, with Raymond Pierrehumbert being insulting rather than discussing the science.
The location where T' is measured does matter. The issue is the magnitude of this error.
Roger -
Yeah, I find the resistance really weird. For certain applications, it's sort of like computing a global average on a lat-lon grid and not bothering to weight by the sine of latitude because it doesn't make much difference in the result.
Maybe we're pushing some people's buttons because of the past nonsense about there supposedly being "no such thing as an average temperature". But whether it's the global average of T or of T^4, it's going up!
Thanks John for the follow up. You are correct that T (and thus T^4) are going up using the global average surface temperature trends analyzed by GISS and others. However, as we show in our JGR paper, there are quite a few issues with the quantitative assessment of the trend including a warm bias.
Moreover, since neither lower tropospheric temperature trends or upper ocean heat content have been increasing in the last several years, it raises questions on the accuracy of using T' (the global average surface temperature) to diagnose global warming (or cooling).
The question of whether the more accurate T^4, weighted spatially, should be used is one of the issues that needs to be included in the discussion. You were the key person who wrote and edited the text with me in our JGR paper on this topic.
Regardless of our views on policy implications regarding the role of humans in the climate system, we need objective assessments of the data. This did not occurr in the 2007 IPCC assessment as I have documented on Climate Science, with the evaluation of the spatial distribution of [T+T']^4 being one example.
John Neilson-Gabon
Lucia's mention of the smallness of (local change of emission)/(local emission) is akin to arguing that global warming is not a problem because the radiative imbalance is only a tiny fraction of the total radiation received or emitted.
John-- actually that's not at all what I meant to imply when I wrote that post. I think context will help here. The post you refer too, when written, was intended to counter an entirely different argument, that appears from time to time on blogs. (Not here.)
At my blog, some visitors were trying to argue that because radiation was T^4, you couldn't disprove the existence of the baseline greenhouse effect (pre-anthro) using the differences in temperature at the surface of the planet. So, their argument was: If there is no baseline greenhouse effect, then there can be no enhanced greenhouse effect due to CO2.
So, in that regard, the importance of T^4 effects on the absolute level of radiation was being used to "disprove" the greenhouse effect by way of disproving the whole thing.
It's an odd argument, but it comes up rather frequently by those who won't write down equations. For that reason, the issue needed to be addressed.
That fact is: You can't disprove the baseline global warming by pointing to T^4 effects. (In fact, you show that if anything, the effect is stronger than you would have thought when ignoring these.)
More context-- and this is the bit that could easily have thrown T and given him the idea that I am playing rhetorical games. (Is that Tamino? Or someone else?)
When I posted the link to that post in comments here, I was a bit confused. I had only read the discussion for Roger's T^4 issue at Atmoz and here. I took it for granted that what Roger's said about T^4 was correctly interpreted by those here and at Atmoz. I later came to realize that was not the case.
Once I realized that the rebuttals there and here have very little to do with what Roger actually says, the thoughts behind my statements did change. With regard to the point Roger is making only anomalies matter. So, in that regard, that particular post, which I linked, early in discussion here in comments, doesn't address the issue you and Roger discussed in your paper.
So, some of what I said did undergo a transition, and I think that wasn't clear in comments. For the confusion associated with that, I apologize.
T,
The odd thing about your response is that even accounting for my change in POV with regard to what Roger said about T^4, nothing you lecture me about has anything to do with anything I posted here in comments or, as far as I'm aware, anywhere.
"Though percentage (or fractional) error is obviously an important consideration when deciding whether a "small approximation" is valid, percentages (ie, fractions) T'/T ARE NOT what one uses to CALCULATE global mean temp anomaly. One uses actual temperature changes (from some baseline) for that."
Who said or thought percent errors T'/T are important to calculating the global mean temp anomaly? I didn't. We are in violent agreement on that.
I think percent errors in the radiation emmitted from the surface do matter when considering whether or not T'/γ is a sufficiently accurate estimator for the increment in radiation leaving the surface as suggested by equation (1) in Eli's quote of Roger's words. In particular, one needs to estimate the magnitude of what is left out of the approximation in 1. In this regard, the percent errors, not in T', but between T'/γ and the full effect are what matter.
...since the climate models do not make the linear approximation (they use the full Stefan Bolztmann) and RP is basically confusing a model with the metric (global mean temp anomaly).
Who said climate models make linear approximation for radiation? Not me. Not Roger. Why would they make that approximation? It would be nutty. I think climate models look like heuristic tools. I realize some here will disagree with me and think they are more. But I don't think GCM's are nutty. Far from it.
But in the context of this discussion: I haven't discussed climate models at all. Roger's paper focuses on empirical issues related to measurement of, T', and to the use of these measurements to evaluate IPCC equation (1). Eli's post doesn't discuss models. So, why do you think anything I've said has to do with models or in anyway contradicts anything Raypierre said?
Finally, I suggest you look at how NASA actually calculates global mean temp anomaly. It does not involve T^4 in any way shape or form.
Did I ever suggest NASA uses T^4 in anyway to estimate T'? No.
And what rhetorical game are you playing? If you are comparing me to the Pielke's I'm flattered. My husband tells me they are both quite bright, and says similar things of Gavin. So, you see, he's objective. :)
Having read a number of different blogs now that link to this thread or comment on it, I'm utterly lost in the flurry.
Has anyone come up with a consensus statement -- something that would fit on one page, with a few hundred footnotes as needed to point to the contentions and claims and corrections made?
I'm looking for something the size of a Letter to Science, the kind that has one paragraph saying mistakes were made, one paragraph stating what's currently agreed on, and a brief final one one dissing those who got the author to agree to admitting something and promising revenge in a subsequent publications, and a polite thankyou to all?
And I'm not even clear whether everyone who's posted long blog pages on this topic would be signing it together, or everyone creates their own.
What's up, Docs?
http://farm3.static.flickr.com/2055/2234432065_f269c1ab4a.jpg?v=0
Ok, a summary (my humble understanding):
Since the rate of infrared emittive power is proportional to T^4, the rate of wattage increase with respects to temperature is proportional to T^3. That is the derivative or one can think it as the "sensitivity" of power to temperature changes. At various temperature points.
As a very very rough estimation, with a 10% bigger temperature (equator vs pole, guesstimate), the power derivative is
1-1.1^3=30% bigger.
Ie if the temperature T at the pole grows 1 Kelvin, the power P grows X Watts, but if the temperature at the equator grows 1 K, the power grows 1.3*X W.
So you get somewhat wrong values of P if you use the "sensitivity" at average T for the whole globe. And vice versa, wrong T for the P.
Another thought experiment: can a planet's average T (temperature) go up while the T^4 (power) goes down? Sure, you lower temperature at the equator and increase it at high latitudes so you have a flatter distribution. The radiating power goes down more at the equator than it increases at the poles. Just a thought experiment. It works the same the other way round.
-
But what is the relevance of this? Climate models of course use much more elaborate models and not just an "average global surface temperature" or the fourth power of that to estimate the radiating power. Ie they take into account that [mean(T)]^4 != mean(T^4).
So it's weird to think this is some new discovery revealing over-estimating global warming or anything. Rather it's just highlighting that there are differences between two simplification levels.
This is more or less what Raypierre was saying already back then when Eli did the original post.
Maybe the whole T vs T^4 debacle could be useful in looking at *outputs* of the models for policy analysis, if the power should be more informative somehow than the temperature? Maybe to some effects.
There are already many visualizations that show temperature colormaps over the world map. These don't suffer from the latitude averaging effect. Well, there are the seasons still... :)
(IPCC AR4 SPM pages 5 and 8 for example)
-
As an additional note, Eli Rabett did some mistakes in his original post. He is a hare of honor of course and has openly admitted and corrected his mistakes.
Post a Comment