The bunny still has pen in paw (cont., cont., cont., cont.,.cont....)
Professor Keller, thank you for your patience. (this is becoming a bit of an obsession, but Ms. Rabett is out of town and the coneys want to play) Today, we would like to explore Essex, et al.'s claim of Contradictory Trends in Global Temperature Averages.
Recall that the authors have claimed that there is no physical basis for preferring one type of average above another, and has defined a series of averages, although this is clearly not as discussed earlier. To demonstrate their claim, they selected data from twelve stations from the GISSTEMP archive.
Phoenix, Arizona; Caragena, Columbia; Dublin, Ireland; Chiang Mai, Thialand; Jan Smuts, South Africa; Honolulu, Hawaii; Sioux Falls, South Dakota; Egedesminde, Greenland; Salehard, Russia; Ceduna, Australia; Halley Antarctica; Souda, IndiaWe have written you previously about the absence of a Souda, India climatology station in the GISS archive. For the purposes of this post, we will omit that station. As you will see this has no effect. Let us return to the definition that is given for the r averages. The s averages will be the same, only worse)
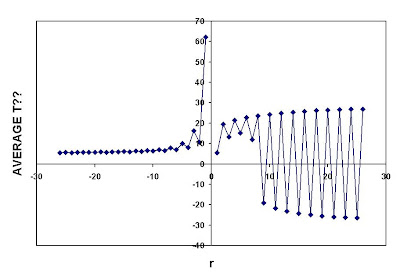
r-mean Average = [1/N (x1^r + x2^r+ ....... +xN^r)]^(1/r) for all rAlthough in principle r could be non-integer, we will assume r integer. If someone has a reason why we should consider r non-integer, he or she should be prepared to deal with roots of negative numbers. Essex, et al., computed monthly means across the stations in Celsius, and a linear trend for each of the monthly averages was fit by ordinary least squares. Trends were displayed for r ranging from -125 to +125 (see Figure 2 in their publication)
As academics, we have all had the experience of students blindly copying numbers from some instrument without questioning whether the apparatus was functioning, and handing in a pretty graph whose information content was nil. Such is Figure 2. While the definitions are clear, Essex, et al., have not considered the physical implications of averages for various values of r, especially in Celsius. This is rather curious in a paper which presumes to establish that there is no physical basis for global temperature anomalies (or even local ones). Even cursory examination shows that
- For even values of r, negative and positive values of temperature contribute the same, positive amount to the average. If one used even r to average a set of negative temperatures, the average would be positive. This is unphysical, and not an acceptable way of averaging Celsius temperatures.
- For values of r above 1, r-averaging for both positive and negative values of r overweights the measurement with largest absolute value. This is not a property one wishes in an statistic that represents the entire set of measurements.
- For negative values of r, r-averaging selects the measurement with the smallest absolute value.
 One can use Kelvin (add 273.16 to all the measurements) in which case there is no possibility of a negative reading, and convergence to the absolute maximum and minimum values is slower as would be expected if one simply expanded the temperatures in Taylor series as T(K)=273.16 + T(C).
One can use Kelvin (add 273.16 to all the measurements) in which case there is no possibility of a negative reading, and convergence to the absolute maximum and minimum values is slower as would be expected if one simply expanded the temperatures in Taylor series as T(K)=273.16 + T(C). At this point the question occurs, did Essex, et al. use Kelvin or Celsius. While have not completed the calculation (the computer mice went off for a St. Patrick's day boozer), the shape of their trend line is indicative......
At this point the question occurs, did Essex, et al. use Kelvin or Celsius. While have not completed the calculation (the computer mice went off for a St. Patrick's day boozer), the shape of their trend line is indicative...... Celsius.
Celsius.Tomorrow we will complete the calculation and explore further physical reasons why Essex, et al.'s treatment of their data set leads to unphysical conclusions.





24 comments:
This illustrates nicely the difference between mediocre mathematicians and physicists, chemists, biologists, pretty much any scientist who regularly deals with the real world (other than to decide what he will have on his toast in the morning, that is).
Scientists always ask themselves "Does this result make sense?"
Mediocre mathematicians are so caught up in the "beauty" of the equation (even ugly equations hacked together with excell), they almost never ask what it means physically.
So they go along their merry way "plugging and chugging".
Don't get me wrong. I like Choo-Choos as much as my 3 year old Nephew. It's just that he understands what some mathematicians do not. You can't put the caboose before the engine -- not if you expect it to go anywhere.
They have not created just one strawman here. They have created an entire army (that stretches to infinity --and beyond), their theory apparently being that if they keep people busy forever knocking down their strawmen, they won't have time to address the physics (if there is any) in their paper. They could be right.
From the claim (made sans proof) that local thermodynamic equlibrium does not apply for air at the surface of the earth (which Eli addressed -- and I just addressed in detail in the comments section of the Open Book Test thread), there is also an unstated claim that follows directly from this: all air temperatures at the surface of the earth are essentially meaningless from a physical standpoint.
Are ME&B really claiming this because it would appear that this is precisely what they are doing if they claim the atmosphere at the surface is not in (local) thermodynamic equilibrium.
Needless to say this is a very interesting (if not supportable) claim.
People have been taking air temperatures at the surface of the earth -- and averaging them -- for a damned long time. Apparently they have been wasting their time and energy!
Scientists, TV weathermen, farmers, fishermen, makers of almanacs and countless others throughout the world have been tracking surface air temperatures for over a century , not because they find it entertaining and have nothing better to do, but with the belief that it actually tells them something about how the weather and climate is behaving within their own locality, country and world at large -- and that this information might help them out in their daily lives (with planting, for example, if one is a farmer).
Silly them. All those farmers who planted in April rather than on January 1? They merely lost out on 3 months of plant growth -- and mountains of cash from crop sales.
Moving beans
and silly means,
We've seen it all,
But wacky Queens.
With loaded dice,
The Three Blind Mice,
A no-name Journal
Did entice.
They toss degrees,
Upon the breeze,
And use the radians,
As they please.
They like their plots,
They like them lots!
And love to play
Connect the dots!
They always use the Centigrade,
For that for which it was not made,
With Kelvin sitting idle,
Rayleigh jeans begin to fade.
They claim that temp
Is so much hemp,
Though it burns,
And makes a heavenly sent.
Eli,
Just a nitpick. Could you not use the word "principal" when you mean "principle", please? This is the second post where you did that.
Principals
With principles,
Are a dozen for a dime,
Capitols,
For Capitals,
Are mistaken all the time.
To is too, and so is two,
But I don't really care, Eli
Do you?
Well yeah, I do try to do better and blush to the tips of my ears when I don't (Pink Rabett syndrome)
2nd anonymous-
A thought experiment-
if you want to get rid of an infinite army of straw men in a queue away from yourself, you start with a flamethrower.
(I'm currently thinking of constructing a 16th century one)
Now, the question is, will the flames leap fromn the front straw man to the one behind him faster than it can step forwards to attack?
Eli said; "Today, we would like to explore Essex, et al.'s claim of Contradictory Trends in Global Temperature Averages.'
Don't you mean "Contradictory claims of Trends in Global Temperature Averages."?
The authors can't seem to settle down on what exactly they are claiming:
Here, they are talking about "earth" (including interior? including atmosphere?):
"Earth does not have just one temperature. It is not in global
thermodynamic equilibrium — neither within itself nor with its surroundings."
Here they are talking about the top of the atmosphere:
"There is also no unique temperature at the top of the atmosphere”.
Here they are talking about "earth as a whole" (as opposed to "earth as a half"? Earth plus atmosphere?):
"The temperature field of the Earth as a whole is not thermodynamically representable by a single temperature."
Here they are talking about non-equilibrium fields in general:
"But an average of
temperature data sampled from a non-equilibrium field is not a temperature."
Here they are talking about a non-equilibrium "system":
"Averaging does not represent any means of avoiding the fact that
a system is not in global thermodynamic equilibrium."
And finally, they talk about all of non-equilibrium thermodynamics:
"Thus, in the case of nonequilibrium thermodynamics, temperature averages fail in the most basic role of an average, which is for one value to represent many."
Each of the above might make an interesting topic of general discussion, but with regard to what climatologists actually do, they are all are irrelevant, since climatologists measure temperatures and calculate mean temperature anomalies (for localities, regions and globally) for air at the surface of the earth. (where Local Thermodynamic Equilibrium applies to a very high degree)
Eli,
Actually, I have reproduced their calculation and, in fairness, they did use Kelvin.
However, the problem is, of course, taking these large positive or negative moments (as denoted by r) is silly. In the limit that r is large and positive, you just get the trend in the maximum (of the twelve station values) for each month. In the limit that r is large and negative, you just get the trend in the minimum for each month. [I have verified this is indeed true....although the convergence for large positive r is slow. The s-values show the asymptotic trend values more clearly.]]
It is worth noting that if you use any reasonable value of r, even r=4 that some claim might be justified if you want to average the radiative energy associated with that temp., you don't get something very different from r=1. In fact, r=4 reduces the trend from 0.060 C per decade to 0.056 C per decade.
The claim about getting different results using different averaging methods is really a tautology.
Of course one does.
So what?
The same goes for lots of different mathematical procedures where there is more than one way of skinning a cat -- not just averaging.
For example, there are several different conventions for combining measurement uncertainties to come up with an overall uncertainty for something that depends on several variables (eg, for volume of box. where there is uncertainty in each of the length, width and height)
If one uses different conventions, one gets a different result. No surprise there. One does not conclude from this that all of them are "meaningless" and that one should therefore toss all the methods. That would be absurd.
That's why there are conventions for doing things that have been decided upon by standards committees and the like.
Even the very things that are used as standards (gage blocks, blackbody sources) must be measured in a particular way to ensure that one gets consistent results.
The idea that one would be able to come up with a uniform system of measurement and subsequent data manipulation (for air temperatures, for example) without such standards is more than a little strange, actually.
If different results are to be comparable, the important thing is not that everyone use one particular method of averaging (selected because it is the "only way", superior to all others)
The important thing is that a method be chosen (and used) that yields results that are internally consistent and that everyone use the same method and in a consistent manner -- or if everyone does not use the same method, that there be a way of accurately converting results from one scheme to another.
Hi Joel, Thanks, I just got through my calculation and put up another post. The main point is that treating the data the way they do leaves most of the variation in seasonal change. If you calculate anomalies you can directly compare trends at places that are at different latitudes and you get a much better error in the slope. Since it was clear that EMA had used Celsius in the water/coffee example, I used that. Fig. 2 and 3 had the trend in K/decade but the text had C.decade. Easy enough to go back and add the offset, but not tonight, and as you say, it does not make a huge difference.
Although the original paper does not properly deal with the issue, it is no excuse for making a stupid post like this. "r-mean Average" is a well-known concept, and with a bit of thinking, you can make it work for both noninteger r and negative numbers. (Your first figure and the text preceeding it are plain drunk)
Hints:
1) Quasi-arithmetic mean
2) x^3=sign(x)*|x|^3
I'm sure you can work out the details.
And since people like Steve Bloom seems to read this blog, let me make this clear: I am not advocating the Essex paper nor I necessarily agree with their conclusions.
Uh, Jean I'd check your assumptions before you accuse Eli of BWI (blogging while intoxicated).
Eli was clearly critiquing the specific paper by Essex et al, using the definition of r-mean that they used (equation number 23) to get their results.
I know. I read the paper.
Did you?
Dear anon, I did read the paper, but did you understand what I wrote?
The problem in Eli's post is that the definition given in the paper (eq 23) only applies if your domain is positive reals. Thus it's fine if you do your calculations in terms of Kelvins, but it's wrong to apply the definition to negative values, as Eli is doing. If you insist on calculating "r-mean average" for a domain containing negative values, you have to change (generalize) your definition. I indicated in my comment how to do that.
"Thus it's fine if you do your calculations in terms of Kelvins, but it's wrong to apply the definition to negative values, as Eli is doing".
There's just one problem. Eli was not the one using Celsius where he should not be (eg, Stefan Boltzman equation). The authors of the paper were.
Jean.
rather than jumping in at the end as you have done, I really think you need to start at the beginning of this conversation and read some of Eli's other posts here to get a context because the author's misuse of Celsius is one of the things that Eli has criticized from the very start.
The paper authors seem to be under the impression that they can use Celsius and Kelvin interchangeably (which is not the case). Some physical formulas (eg, Stefan Boltzmann equation) demand Kelvin. There is no option of using Celsius (period).
If you want to deseasonalize the data (as we saw in the next chapter) you have to deal with negative numbers as well as positive, and that dear Jean is a damn good reason for going with the simple arithmetic average, besides the fact that the other averages do not equally weight the data from each station/grid point.
Oh yeah, if you use the sign(x)*x^3, or absolute value you have the five years of losses average to a gain problem when you use Celsius. Not a problem with Kelvin, otoh you then buy into the overweighting of the largest values in the set and you still have the seasonal variation to deal with which makes the situation worseEli suggests Jean run some examples to convince herself.
Dear Eli, I'm rather dissappointed of your answer. I was under impression that you are one of the most capable of these AGW-bloggers.
I think you should really take your head out of sand, or how you say it. If a method is used by Essex et al, it does not make the method itself bad, no matter how much you dislike the authors or how bad the paper is. The f-mean is a well-known concept, and trying to make it look like something stupid invented by Essex et al does not make any good to you. It only makes you look stupid. If you want to argue that only arithmetic mean (f is an identity map) is meaningful in this context (I might even agree), that's fine, but do it without distorting mathematical facts. Th fact is, and remains, that the "r averages" definition given in the paper, and used by you, only applies if your domain consists of positive numbers. Essex et al, seems to assume that although they are very unclear about it.
In any case, if you want to take "r average" over intervals containing negative numbers, you have to extend your definition. Since you didn't get it from the hints, here it is explicitly: take f(x)=sign(x)abs(x)^r in the definition of the f-mean (first link I gave you), and you are in business. No "five years of losses average to a gain"-problem. Your first figure and the text preceeding it are simply wrong, and belittling me or someone else saying it to you does not change the fact.
Jean said: "Essex et al, seems to assume that although they are very unclear about it."
Clear as mud, since they use Celsius for temps associated with Stefan Boltzmann elsewhere in the paper -- a real hoot (to chemists and physicists, if not mathematicians)
You also said that
"The f-mean is a well-known concept, and trying to make it look like something stupid invented by Essex et al does not make any good to you[sic]"
Just a minor nitpick : I assume what you meant to say is that this "does not make you look very good", or "this makes you look very bad". (???)
I would just point out that what Jean is arguing here is a sidetrack.
It does not address the paper by Essex et al (or at all).
Indeed, the opposite is true, since they were essentially implying that for the case at hand, all averaging methods were created equal and that there is therefore no reason to choose one over another.
That is clearly not the case.
Perhaps Jean would like to comment on the main claims of the paper and not just on mathematical trivia.
It is instructive to focus on the region of the "Trends through r-means" graph that is above zero (corresponding to trend of increasing mean temperature anomaly) because, notwithstanding the claims of the paper authors, there are good physical reason for doing so.
This region corresponds to r-values roughly between about -6 to +15.
This region corresponds to the power to which T (or more precisely, delta-T) is raised in the averaging formula , of course, which also just happens to encompass the power to which "T" appears in fundamental physical formulas (eg, ideal gas equation, Stefan-Boltzmann equation, equation relating average energy per molecule to temperature in a gas in local thermodynamic equilibrium, etc).
In fact, T normally appears in such physical formulas raised to either power "1" (ideal gas) or to power "4" (Stefan Boltzmann)
Nowhere in any fundamental physical formula does temperature ever appear raised to a power < -6 or > 15 (to say the least).
The paper's authors have made great hay of the fact that the vast majority of possible r-values (an infinite number of them, in fact) lie outside this range. But so what?
What possible physical justification could there ever be for utilizing an averaging formula that uses an r-value outside that range? (ie, r < -6 and r > 15)
As pointed out above, the higher powers tend to over-weight the extreme values and this is completely unjustified in a case in which one has no reason to suspect that some values should take on greater weight than others. In fact, doing so in such a case would defeat the whole purpose of averaging.
The underlying (implicit) assumption in the paper is that the power to which T appears in fundamental physical formulas is not relevant to the selection of an averaging method because those formulas do not apply when local thermodynamic equilibrium is not satisfied.
That assumption is completely unwarranted. The authors make several broad (sweeping) statements in their paper regarding "non-equilibrium thermodynamics" in general and how it applies to the "earth as a whole", but nowhere do they address the issue that they should be addressing: air at the surface of the earth, which is what climate scientists take the temperature of, after all -- and which, as it turns out, is in local thermodynamic equilibrium to a high degree of approximation.
See comments (ie, calculations) on that subject at the end of the Open book test post" here
Post a Comment