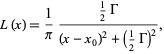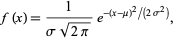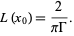Holland and Webster in the Philosophical Transactions of the Royal Society
We find that long-period variations in tropical cyclone and hurricane frequency over the past century in the North Atlantic Ocean have occurred as three relatively stable regimes separated by sharp transitions. Each regime has seen 50% more cyclones and hurricanes than the previous regime and is associated with a distinct range of sea surface temperatures (SSTs) in the eastern Atlantic Ocean. Overall, there appears to have been a substantial 100-year trend leading to related increases of over 0.78C in SST and over 100% in tropical cyclone and hurricane numbers. It is concluded that the overall trend in SSTs, and tropical cyclone and hurricane numbers is substantially influenced by greenhouse warming. Superimposed on the evolving tropical cyclone and hurricane climatology is a completely independent oscillation manifested in the proportions of tropical cyclones that become major and minor hurricanes. This characteristic has no distinguishable net trend and appears to be associated with concomitant variations in the proportion of equatorial and higher latitude hurricane developments, perhaps arising from internal oscillations of the climate system. The period of enhanced major hurricane activity during 1945–1964 is consistent with a peak period in major hurricane proportionsIt's a hot time out there in the Atlantic today
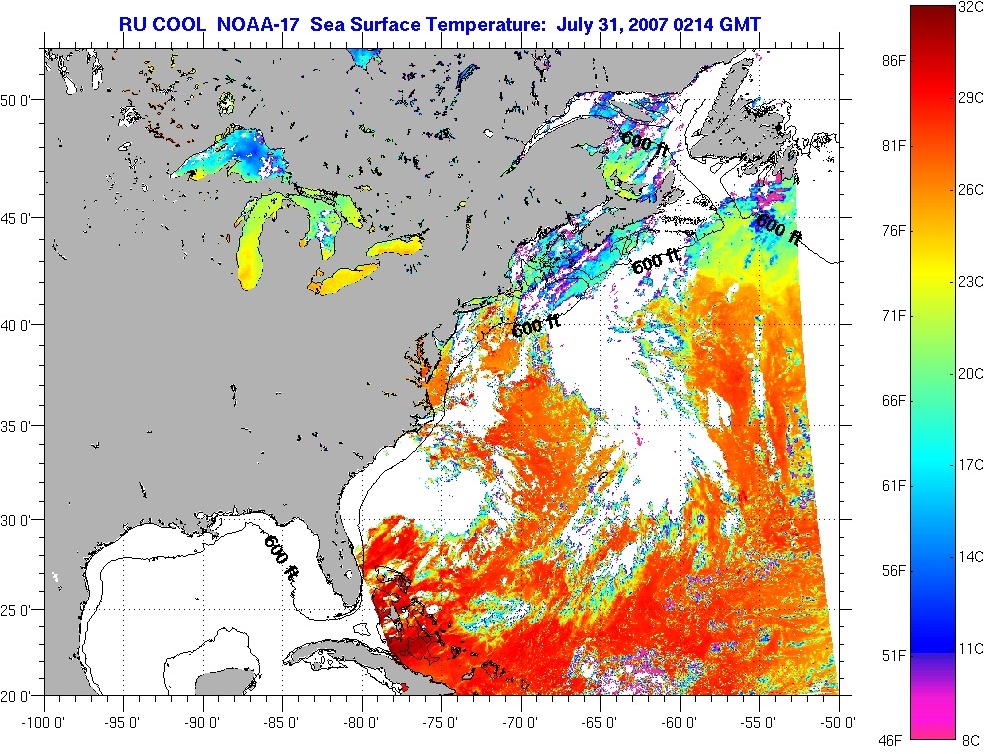 and the Gulf is turning into a hibatchi.
and the Gulf is turning into a hibatchi.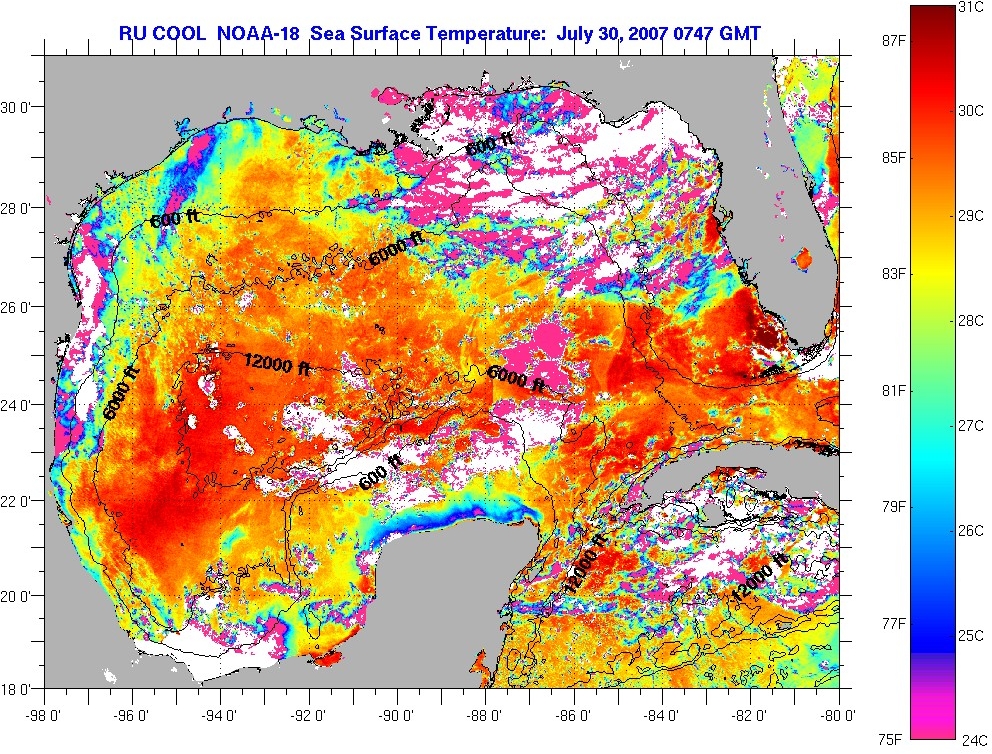
Those of you without access to Phil. Trans. can read a preprint version